Parallelogram. Formulas and Properties of a Parallelogram

Page Navigation: Definition of a parallelogram Characterizations of a parallelogram The basic properties of a parallelogram The sides of a parallelogram The diagonal of a parallelogram The perimeter of a parallelogram The area of a parallelogram

Definition.

Parallelogram is a quadrilateral whose opposite sides are parallel and pairwise equal(lie on parallel lines)..

Parallelograms differ in size of an adjacent sides and angles but opposite angles is equal.


Fig.1		Fig.2

Characterizations of a parallelogram

Quadrilateral ABCD is a parallelogram, if at least one of the following conditions:

1. Quadrilateral has two pairs of parallel sides:
AB||CD, BC||AD

2. Quadrilateral has a pair of parallel sides with equal lengths:
AB||CD, AB = CD (или BC||AD, BC = AD)

3. Opposite sides are equal in the quadrilateral:
AB = CD, BC = AD

4. Opposite angles are equal in the quadrilateral:
∠DAB = ∠BCD, ∠ABC = ∠CDA

5. Diagonals bisect the intersection point in the quadrilateral:
AO = OC, BO = OD

6. The sum of the quadrilateral angles adjacent to any side is 180°:
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠ABC = 180°

7. The sum of the diagonals squares equals the sum of the sides squares in the quadrilateral:
AC² + BD² = AB² + BC² + CD² + AD²

The basic properties of a parallelogram

Square, rectangle and rhombus is a parallelogram.

1. Opposite sides of a parallelogram have the same length:

AB = CD, BC = AD

2. Opposite sides of a parallelogram are parallel:

AB||CD, BC||AD

3. Opposite angles of a parallelogram are equal:

∠ABC = ∠CDA, ∠BCD = ∠DAB

4. Sum of the parallelogram angles is equal to 360°:

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

5. The sum of the parallelogram angles adjacent to any sides is 180°:
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠ABC = 180°

6. Each diagonal divides the parallelogram into two equal triangle

7. Two diagonals is divided parallelogram into two pairs of equal triangles

8. The diagonals of a parallelogram intersect and intersection point separating each one in half:

AO = CO =	d₁
	2
BO = DO =	d₂
	2

9. Intersection point of the diagonals is called a center of parallelogram symmetry

10. Sum of the diagonals squares equals the sum of sides squares in parallelogram:
AC² + BD² = 2AB² + 2BC²

11. Bisectors of parallelogram opposite angles are always parallel

12. Bisectors of parallelogram adjacent angles always intersect at right angles (90°)

The sides of a parallelogram

Sides of a parallelogram formulas:

1. Formula of parallelogram sides in terms of diagonal and angle between the diagonals:

a =	√d₁² + d₂² - 2d₁d₂·cosγ	=	√d₁² + d₂² + 2d₁d₂·cosδ
	2		2

b =	√d₁² + d₂² + 2d₁d₂·cosγ	=	√d₁² + d₂² - 2d₁d₂·cosδ
	2		2

2. Formula of parallelogram sides in terms of diagonals and other side:

a =	√2d₁² + 2d₂² - 4b²
	2

b =	√2d₁² + 2d₂² - 4a²
	2

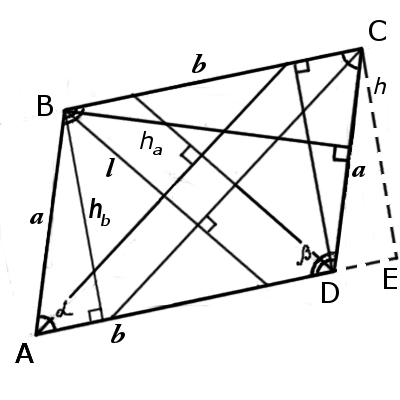
3. Formula of parallelogram sides in terms of altitude (height) and sine of an angle:

a =	h_b
	sin α

b =	h_a
	sin α

4. Formula of parallelogram sides in terms of area and altitude (height):

a =	A
	h_a

b =	A
	h_b

The diagonal of a parallelogram

Definition.

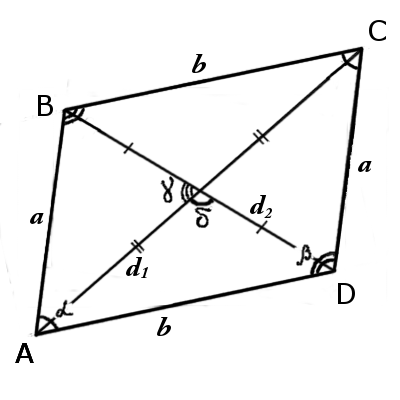
The diagonal of a parallelogram is any segment that connects two vertices of a parallelogram opposite angles.

Parallelogram has two diagonally - a longer let be d₁, and shorter - d₂

Diagonal of a parallelogram formulas:

1. Formula of parallelogram diagonal in terms of sides and cosine β (cosine theorem)

d₁ = √a² + b² - 2ab·cosβ d₂ = √a² + b² + 2ab·cosβ

2. Formula of parallelogram diagonal in terms of sides and cosine α (cosine theorem)

d₁ = √a² + b² + 2ab·cosα d₂ = √a² + b² - 2ab·cosα

3. Formula of parallelogram diagonal in terms of two sides and other diagonal:

d₁ = √2a² + 2b² - d₂²
d₂ = √2a² + 2b² - d₁²

4. Formula of parallelogram diagonal in terms of area, other diagonal and angles between diagonals:

d₁ =	2A	=	2A
	d₂·sinγ		d₂·sinδ

d₂ =	2A	=	2A
	d₁·sinγ		d₁·sinδ

The perimeter of a parallelogram

Definition.

The perimeter of a parallelogram is the sum of the all parallelogram sides lengths.

Perimeter of a parallelogram formulas:

1. Formula of parallelogram perimeter in terms of sides:

P = 2a + 2b = 2(a + b)

2. Formula of parallelogram perimeter in terms of one side and diagonals:

P = 2a + √2d₁² + 2d₂² - 4a²
P = 2b + √2d₁² + 2d₂² - 4b²

3. Formula of parallelogram perimeter in terms of side, height and sine of an angle:

P =	2(b +	h_b	)
		sin α

P =	2(a +	h_a	)
		sin α

The area of a parallelogram

Definition.

The area of a parallelogram the space is restricted parallelogram sides or within the perimeter of a parallelogram.

Area of a parallelogram formulas:

1. Formula of parallelogram area in terms of side and height:

A = a · h_a
A = b · h_b

2. Formula of parallelogram area in terms of sides and sine of an angle between this sides:

A = ab sinα
A = ab sinβ

3. Formula of parallelogram area in terms of diagonals and sine of an angle between diagonals:

A =	1	d₁d₂ sin γ
	2

A =	1	d₁d₂ sin δ
	2

Geometry formulas Square. Formulas and Properties of a Square Rectangle. Formulas and Properties of a Rectangle Parallelogram. Formulas and Properties of a Parallelogram Rhombus. Formulas and Properties of a Rhombus Circle, disk, segment, sector. Formulas and properties Ellipse. Formulas and properties of ellipse Cylinder. Formulas and properties of a cylinder Cone. Formulas, characterizations and properties of a cone Area. Formulas of area Perimeter. Formulas of perimeter Volume. Formulas of volume Surface Area Formulas

All tables and Formulas

Add the comment