OnlineMSchool
Study of mathematics online.
Study math with us and make sure that "Mathematics is easy!"
Sign in Log in Log out

Rhombus. Formulas, characterizations and properties of rhombus

Page Navigation: Definition of rhombus Characterizations of rhombus Basic properties of rhombus Side of rhombus Diagonals of rhombus Perimeter of rhombus Area of rhombus Inradius of rhombus
Definition.
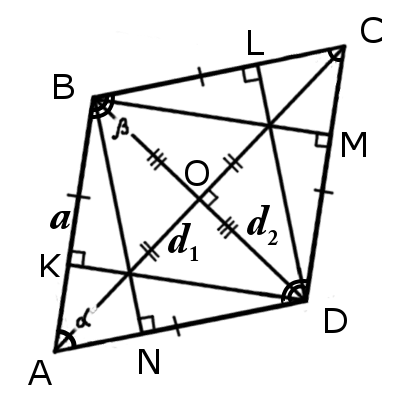
Rhombus is a parallelogram that has equal side. If the diamond angles is straight, then it is a square.
Rhombus differ in the size of side and the size of angles.
Rhombus. Image with marks Rhombus. Image with marks
Fig.1 Fig.2

Characterizations of rhombus

Parallelogram ABCD is a rhombus if at least one of the following conditions:
1. Two consecutive sides are equal in length (it follows that all sides are the same):
АВ = ВС = СD = AD
2. If the diagonals are perpendicular:
AC┴BD
3. If the diagonals (angle bisectors) bisects an interior angles:
∠BAC = ∠CAD or ∠BDA = ∠BDC
4. If all the parallelogram heights have equal lenght:
BN = DL = BM = DK
5. If the parallelogram divided by diagonals into four equal rectangular triangles:
Δ ABO = Δ BCO = Δ CDO = Δ ADO
6. If in parallelogram can be inscribed circle.

Basic properties of rhombus

1. It has all the properties of a parallelogram
2. A diagonals are perpendicular:
AC┴BD
3. A diagonals is angle bisectors:
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
4. The sum of the squares of the diagonals equals the sum of the squares of the sides (the parallelogram law):
AC2 + BD2 = 4AB2
5. The crosspoint of the diagonals is the center of symmetry.
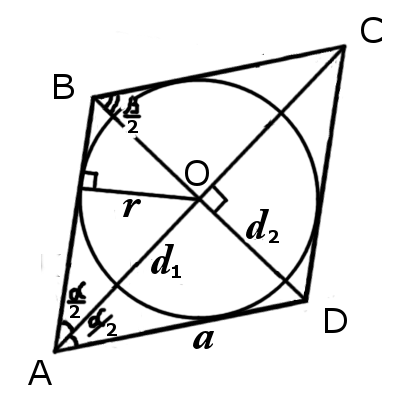
6. At any rhombus can be inscribed circle.
7. The center of incircle is the diagonals crosspoint.

Side of rhombus

Side of rhombus formulas:

1. Formula of rhombus side in terms of area and height:
a = S
ha
2. Formulas of rhombus side in terms of area and sine of any angle:
a = √S
√sinα
a = √S
√sinβ
3. Formula of rhombus side in terms of area and inradius:
a = S
2r
4. Formula of rhombus side in terms of it diagonals:
a = √d12 + d22
2
5. Formulas of rhombus side in terms of diagonal and cosine of angle (cosα or cosβ):
a = d1
√2 + 2 cosα
a = d2
√2 - 2 cosβ
6. Formulas of rhombus side in terms of longer diagonal and half-angle:
a = d1
2cos(α/2)
a = d1
2sin(β/2)
7. Formulas of rhombus side in terms of smaller the diagonal and half-angle:
a = d2
2cos(β/2)
a = d2
2sin(α/2)
8. Formula of rhombus side in terms of perimeter:
a = Р
4

Diagonals of rhombus

Definition.
Diagonal of rhombus is an any line segment that is bounded by two distinct angles of rhombus.
Rhombus has two diagonals the longer d1, and the smaller d2

Diagonals of a rhombus formulas:

1. Formulas of rhombus longer diagonal in terms of side and cosine of any angle (cosα or cosβ)

d1 = a√2 + 2 * cosα
d1 = a√2 - 2 * cosβ
2. Formulas of rhombus smaller diagonal in terms of side and cosine of any angle (cosα or cosβ)

d2 = a√2 + 2 * cosβ
d2 = a√2 - 2 * cosα
3. Formulas of rhombus longer diagonal in terms of side and half-angle:

d1 = 2a * cos(α/2)
d1 = 2a * sin(β/2)
4. Formulas of rhombus smaller diagonal in terms of side and half-angle:

d2 = 2a * sin(α/2)
d2 = 2a * cos(β/2)
5. Formulas of rhombus diagonal in terms of side and other diagonal:

d1 = √4a2 - d22
d2 = √4a2 - d12
6. Formulas of rhombus diagonal in terms of other diagonal and tangents of half-angle:

d1 = d2 * tg(β/2)
d2 = d1 * tg(α/2)
7. Formulas of rhombus diagonal in terms of area and other diagonal:

d1 = 2S
d2
d2 = 2S
d1
8. Formulas of rhombus diagonals in terms of sine of half-angle and inradius:

d1 = 2r
sin(α/2)
d2 = 2r
sin(β/2)

Perimeter of rhombus

Definition.
Perimeter of rhombus is the sum of all sides lenght of rhombus.

The lenght of side of rhombus can be find by the formulas listed above.

Perimeter of a rhombus formula:

Formula of rhombus perimeter in terms of rhombus side:

P = 4a

Area of rhombus

Definition.
The area of rhombus is the space limited by sides of rhombus, within the perimeter of rhombus.

Area of a rhombus formulas:

1. Formula of rhombus area in terms of side and height:

S = a · ha
2. Formula of rhombus area in terms of side and sine any angles:

S = a2 · sinα
3. Formula of rhombus area in terms of side and inradius:

S = 2a · r
4. Formula of rhombus area in terms of two diagonals:

S = 1d1d2
2
5. Formula of rhombus area in terms of sine angles and inradius:

S = 4r2
sinα
6. Formulas of rhombus area in terms of diagonal and the tangents half-angle:

S = 1d12 · tg(α/2)
2
S = 1d22 · tg(β/2)
2

Incircle of a rhombus

Definition.
Incircle of a rhombus is the largest circle contained in the rhombus and it touches the four sides of a rhombus. The center of the incircle is called the rhombus'es incenter and disposed on the crosspoint of diagonales.

Inradius of a rhombus formulas:

1. Formula of rhombus inradius in terms of height:

r = h
2
2. Formula of rhombus inradius in terms of area and the side:

r = S
2a
3. Formula of rhombus inradius in terms of area and sine angles:

r = √S · sinα
2
4. Formulas of rhombus inradius in terms of side and sine any angles:

r = a · sinα
2
r = a · sinβ
2
5. Formulas of rhombus inradius in terms of diagonal and sine half-angle:

r = d1 · sin(α/2)
2
r = d2 · sin(β/2)
2
6. Formula of rhombus inradius in terms of rhombus diagonals:

r = d1 · d2
2√d12 + d22
7. Formula of rhombus inradius in terms of rhombus diagonals and side:

r = d1 · d2
4a

Geometry formulas Square. Formulas and Properties of a Square Rectangle. Formulas and Properties of a Rectangle Parallelogram. Formulas and Properties of a Parallelogram Rhombus. Formulas and Properties of a Rhombus Circle, disk, segment, sector. Formulas and properties Ellipse. Formulas and properties of ellipse Cylinder. Formulas and properties of a cylinder Cone. Formulas, characterizations and properties of a cone Area. Formulas of area Perimeter. Formulas of perimeter Volume. Formulas of volume Surface Area Formulas
All tables and Formulas

Add the comment

0
Follow OnlineMSchool on