Triangle Area Calculator (9 diferent ways)
This free online calculator will help you to find the area of a triangle (9 different ways).
Using this online calculator, you will receive a detailed step-by-step solution to your problem, which will help you understand the algorithm how to find triangle area.
Calculation of Triangle Area
 Select method (defined data):
Select method (defined data):
Input data:
a =
b =
c =
c =
Area in
Entering data into the triangle area calculator
To calculate the area of a triangle:
- select defined datas;
- enter the value of datas;
- select units of measurement - meter (m), centimeter (cm) or millimeter (mm);
- select in which units you want to get the area - square meters (m2), square centimeters (cm2) or square millimeters (mm2).
You can input only integer numbers or fractions in this online calculator. More in-depth information read at these rules.
If you have any difficulties with units conversion, you can use the length converter and area converter.
Additional features of triangle area calculator
- Use and keys on keyboard to move between field in calculator.
You can find the area of a triangle if you know the following values:
- Lengths of the three sides (using Heron's formula)
- Lengths of the two sides and angle between them
- Lengths of the base of the triangle, and altitude of the triangle
- Lengths of the three sides and circumradius
- Lengths of the three sides and in-radius
- Lengths of the semiperimeter and in-radius
- Lengths of the two sides of triangle and angle
- Length of the side of triangle and two angles
- Length of the circumradius and two angles
Theory. Triangle Area
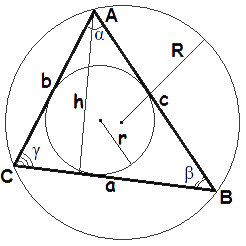
The formulas for calculating the area of a triangle
- Area of a triangle when we know the base and the height
The area of a triangle is equal to half of base times height.
A =
1 2 - Area of a triangle when we know the lengths of all three of its sides
Heron's formula
A = √s(s - a)(s - b)(s - c)
- Area of a triangle when we know two sides and the included angle
The area of a triangle is equal to half of a product of two sides and sine of the angle between this sides.
A =
1 2 - Area of a triangle when we know three sides and circumradius
A =
a · b · с 4R - Area of a triangle when we know semiperimeter and in-radius
The area of a triangle is equal to semiperimeter times in-radius.
A = s · r
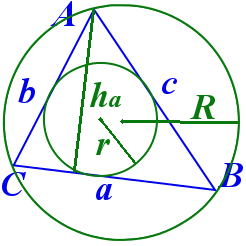
where A - the area of a triangle,
a, b, c - the length of sides BC,AC,AB accordingly,
h - the height, the length of the altitude,
γ - the angle between sides a and b,
r - the length of the in-radius,
R - the length of the circumradius,
s - the semiperimeter, or half of the triangle's perimeter.
You can input only integer numbers, decimals or fractions in this online calculator (-2.4, 5/7, ...). More in-depth information read at these rules.
Try online calculators for calculation of geometrical figures areaTriangle Area Calculator (9 diferent ways)Online calculator. Triangle area. Heron's formulaQuadrilateral Area CalculatorSquare Area CalculatorRectangle Area CalculatorParallelogram Area CalculatorRhombus Area CalculatorTrapezium Area CalculatorCircle Area CalculatorEllipse Area CalculatorShow all online calculators
See also
Triangle. Formulas, characterizations and properties of triangle
Area Formulas for Geometric Figures.
Length and width converter
Area converter
Perimeter calculators
Add the comment
