Square. Formulas and Properties of a Square

Page Navigation: Definition of a square The basic properties of a square Diagonal of a square The perimeter of a square The area of a square The circumscribed circle of a square (circumcircle) The inscribed circle of a square (incircle)

Definition.

Square is a regular quadrilateral in which all four sides and angles are equal. Squares differ only in sides length but all four angles is right angles.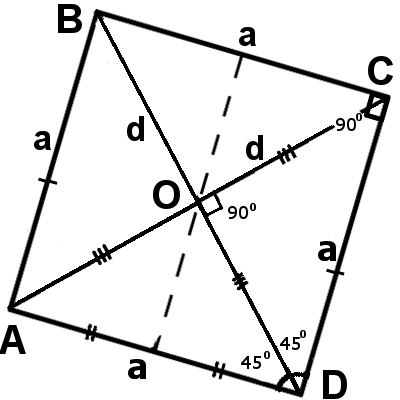


Fig.1		Fig.2

The basic properties of a square

Squares can also be a parallelogram, rhombus or a rectangle if they have the same length of diagonals, sides and right angles.

1. All four sides of a square are same length, they are equal:

AB = BC = CD = AD:

AB = BC = CD = AD

2. Opposite side of a square are parallel:

AB||CD, BC||AD

3. All four angles of a square are right angles:

∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°

4. Sum of the angles of a square are equal to 360 degrees:

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

5. Diagonal of a square are same length:

AC = BD

6. Each diagonal of a square divides its into two equal symmetrical area

7. Diagonals of a square intersect its right angles, and share each other half:

AC┴BD		AO = BO = CO = DO =	d
			2

8. Intersection point of the diagonals is called the center of the square and also the circumcenter of the inscribed circle and circumscribed circle

9. Each diagonal divides the angle of the square in half, meaning they are bisectors of the angles of the square:

ΔABC = ΔADC = ΔBAD = ΔBCD
∠ACB = ∠ACD = ∠BDC = ∠BDA = ∠CAB = ∠CAD = ∠DBC = ∠DBA = 45°

10. Both diagonals divide the square into four equal triangle besides these triangles are both isosceles and rectangular:

ΔAOB = ΔBOC = ΔCOD = ΔDOA

Diagonal of a square

Definition.

Diagonal of the square is any segment that connects two vertices opposite angles of the square.

Diagonal of any square is always greater than its side √2 times.

Diagonal of a square formulas

1. Formula of the square diagonal in terms of the square side:
d = a·√2

2. Formula of the square diagonal in terms of the square area:
d = √2A

3. Formula of the square diagonal in terms of the square perimeter:

d =	P
	2√2

4. formula of the square diagonal in terms of the circumradius:
d = 2R

5. formula of the square diagonal in terms of the diameter of the circumcircle:
d = D_c

6. formula of the square diagonal in terms of the inradius:
d = 2r√2

7. formula of the square diagonal in terms of the diameter of the incircle:
d = D_i√2

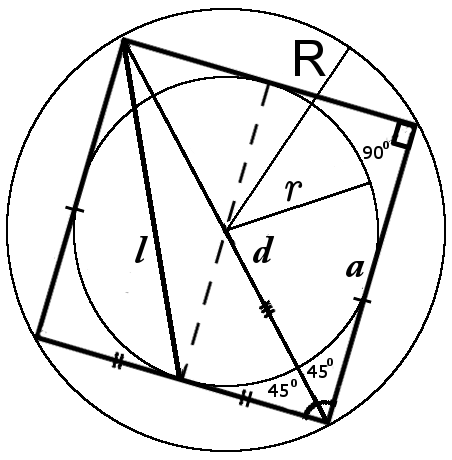
8. formula of the square diagonal in terms of the length of the segment l (Fig.2):

d = l	2√10
	5

The perimeter of a square

Definition.

The perimeter of a square called the sum of the lengths of all sides of the square.

Perimeter of a square formulas

1. Formula of the square perimeter in terms of the square side: P = 4a

2. Formula of the square perimeter in terms of the square area: P = 4√A

3. Formula of the square perimeter in terms of the square diagonal: P = 2d√2

4. Formula of the square perimeter in terms of the circumradius: P = 4R√2

5. Formula of the square perimeter in terms of the diameter of the circumcircle: P = 2D_c√2

6. Formula of the square perimeter in terms of the inradius: P = 8r

7. Formula of the square perimeter in terms of the diameter of the incircle: P = 4D_i

8. Formula of the square perimeter in terms of the length of the segment l (Fig.2):

P = l	8
	√5

The area of a square

Definition.

Area of the square is called the space is limited to the square of the parties, that is, within the perimeter of a square.

The area of a square larger than area of any quadrilateral with the same perimeter.

Area of a square formulas

1. Formula of the square area in terms of the square side:A = a²

2. Formula of the square area in terms of the square perimeter:

A =	P²
	16

3. Formula of the square area in terms of the square diagonal:

A =	d²
	2

4. Formula of the square area in terms of the circumradius:A = 2R²

5. Formula of the square area in terms of the diameter of the circumcircle:

A =	D_c²
	2

6. Formula of the square area in terms of the inradius: A = 4r²

7. Formula of the square area in terms of the diameter of the incircle: A = D_i²

8. Formula of the square area in terms of the length of the segment l (Fig.2):

A = l ²	16
	√5

The circumscribed circle of a square

Definition.

The circumscribed circle of a square (circumcircle) called circle which passes only four top corners of the square and has a center at the intersection of the diagonals of the square.

The circumradius lager then inradius fo √2 times.

The circumradius equal to half the diagonal.

The area of the circumcircle larger then area of the same square at is π/2 times.

Circumradius of a square formulas

1. Formula of the square circumradius in terms of the square side:

R = a	√2
	2

2. Formula of the square circumradius in terms of the square perimeter:

R =	P
	4√2

3. Formula of the square circumradius in terms of the square area:

R =	√2A
	2

4. Formula of the square circumradius in terms of the square diagonal:

R =	d
	2

5. Formula of the square circumradius in terms of the diameter of the circumcircle:

R =	D_c
	2

6. Formula of the square circumradius in terms of the inradius: R = r √2

7. Formula of the square circumradius in terms of the diameter of the incircle:

R = D_i	√2
	2

8. Formula of the square circumcircle in terms of the length of the segmentl (Fig.2):

R = l	√10
	5

The inscribed circle of a square

Definition.

The inscribed circle of a square (incircle) called the circle is tangent to the middle of the square sides and a circumcenter at the intersection of the diagonals of the square.

The inradius equal to half a square side.

The area of a incircle smaller than area of the square is 4/π times.

Inradius of a square formulas

1. Formula the square inradius in terms of the square side:

r =	a
	2

2. Formula the square inradius in terms of the square diagonal:

r =	d
	2√2

3. Formula the square inradius in terms of the square perimeter:

r =	P
	8

4. Formula the square inradius in terms of the square area:

r =	√A
	2

5. Formula the square inradius in terms of the circumradius:

r =	R
	√2

6. Formula the square inradius in terms of the diameter of the circumcircle:

r =	D_c
	2√2

7 Formula the square inradius in terms of the diameter of the incircle:

r =	D_i
	2

8. Formula the square inradius in terms of the length of the segmentl (Fig.2):

r =	l
	√5

Geometry formulas Square. Formulas and Properties of a Square Rectangle. Formulas and Properties of a Rectangle Parallelogram. Formulas and Properties of a Parallelogram Rhombus. Formulas and Properties of a Rhombus Circle, disk, segment, sector. Formulas and properties Ellipse. Formulas and properties of ellipse Cylinder. Formulas and properties of a cylinder Cone. Formulas, characterizations and properties of a cone Area. Formulas of area Perimeter. Formulas of perimeter Volume. Formulas of volume Surface Area Formulas

All tables and Formulas

Add the comment