Circle, disk, segment, sector. Formulas, characterizations and properties of circle
- Circle - definition
- Disk - definition
- Radius and diameter of a circle
- Properties of a circle
- Area and circumference of circle
- The equation of circle
- Tangent of circle and its properties
- Secant of circle and its properties
- Chord of circle and its properties
- Central angle and inscribed angle of a circle and its properties
- Arc of a circle, length of arc, subtending angle of an arc
- Semicircle and semidisc
- Sector, area of sector
- Segment, area of segment
- Concentric circle
- Annulus
 |
 |
 |
Definition. Circle is a set of all points in the plane which are equidistant from a given point О, called the center of circle.
Definition. Unit circle is a circle, whose radius is equal to one.
Definition. Disk is part of the plane bounded by circle.
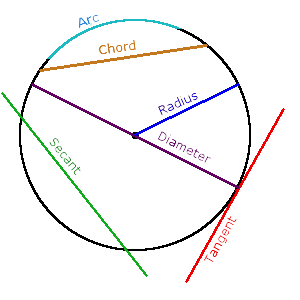
Definition. Radius of circle R is the distance from the circle center О to any point on the circle.
Definition. Diameter of circle D is a segment that connects two points on circle and passes through its center.
Properties of a circle
1. Diameter of circle is equal two radiuses.
D = 2r
2. The shortest distance from the center circle to the secant (chord) is always smaller radius.
3. Three points that not placed on a straight line can hold only one circle.
4. Among all closed curves of equal length, circle has the largest area.
5. If two circle touch at one point, this point placed on the line that passes through the centers of the circles.
Area and circumference of circle
Length of circumference
1. Formula of the circumference length in terms of the diameter:
C = πD
2. Formula of the circumference length in terms of the radius:
C = 2πr
Formula of the circle area
1. Formula of the circle area in terms of the radius:
A = πr2
2. Formula of the circle area in terms of the diameter:
A =
The equation of circle
1. The equation of circle with radius r and center at the start of Cartesian coordinate:
r2 = x2 + y2
2. The equation of circle with radius r and center at point with coordinates (a, b) in the Cartesian coordinate:
r2 = (x - a)2 + (y - b)2
3. Parametric equations of circle with a radius r and center at point with coordinates (a, b) in the Cartesian coordinate:
| { | x = a + r cos t |
| y = b + r sin t |
Tangent of circle and its properties
Definition. Tangent is a coplanar straight line that touches the circle at a single point.
Tangent properties
1. Tangent is always perpendicular to the radius of the circle drawn at the point of contact.
2. The shortest distance from the center of circle to tangent is radius of the circle.
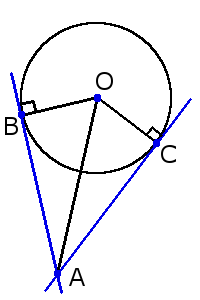
AB = AC
Also, if you draw a line through the center O and the intersection point A of these tangents, the angles between this line and tangents will be equal:∠ОAС = ∠OAB
Secant of circle and its properties
Definition. Secant of a circle is a straight line, connecting two points of circle.
Properties of circle secant

AQ ∙ BQ = CQ ∙ DQ

AQ ∙ BQ = CQ2
Chord of circle and its properties
Definition. Chord of a circle is a segment that connects two points of circle. Chord is a segment of tangent.
Length of chord

AB = 2r sin

AB = 2r sin α
Chord properties

if chords AB = CD, then
arc ◡ AB = ◡ CD
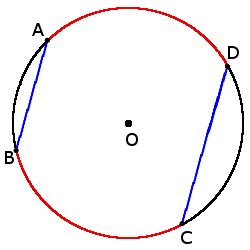
if chords AB ∣∣ CD, then
◡ AD = ◡ BC
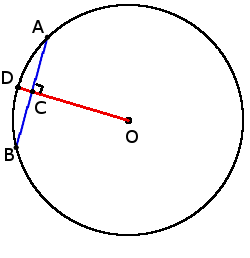
if OD ┴ AB, then
AC = BC
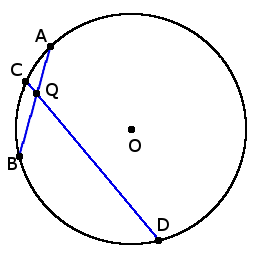
AQ ∙ BQ = DQ ∙ QC
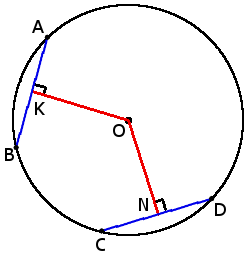
if chords AB = CD, then
ON = OK
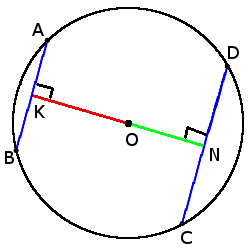
if CD > AB, then
ON < OK
Central angle and inscribed angle of a circle and its properties
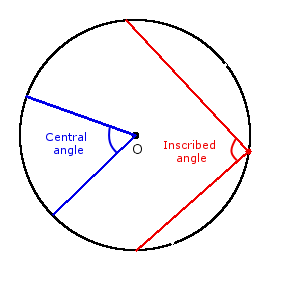
Definition. Central angle circle is the angle, the apex of which is the center of circle.
Definition. Inscribed angle is the angle inside the circle, the apex of which lies on the circle.
Angle properties
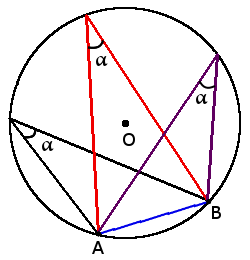
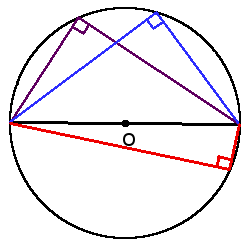

β =

α + β = 180°
Definition. Arc of a circle (◡) is part of the circle, connecting two points on the circle.
Definition. Subtending angle of an arc is angle between two radii which limit this arc. Subtending angle arc is always equal the central angle between radii, which limits end points this arc.
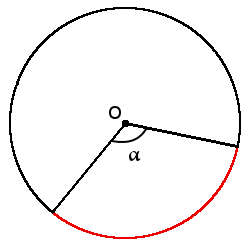
l =
Definition. Semicircle is arc whose ends are connected by diameter of a circle.
Definition. Semidisc (◓) is part of the disk, which is bounded by a semicircle and diameter.
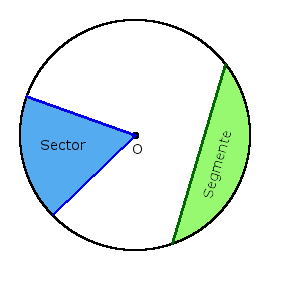
Definition. Sector (◔) is part of the disk, which is bounded by two radii and an arc between the radii.

A =
Definition. Segment is part of the disk, which is bounded by the arc and the chord connecting the ends of this arc.
Definition. Concentric circle is circle with different radii whish having a common center.
Definition. Annulus is part of the plane bounded by two concentric circles.
Geometry formulas
Square. Formulas and Properties of a Square
Rectangle. Formulas and Properties of a Rectangle
Parallelogram. Formulas and Properties of a Parallelogram
Rhombus. Formulas and Properties of a Rhombus
Circle, disk, segment, sector. Formulas and properties
Ellipse. Formulas and properties of ellipse
Cylinder. Formulas and properties of a cylinder
Cone. Formulas, characterizations and properties of a cone
Area. Formulas of area
Perimeter. Formulas of perimeter
Volume. Formulas of volume
Surface Area Formulas
Add the comment