Formulas and properties of nth root

The nth root of the number a is a number b, n-th power is equal to a

The following properties hold for nth root (a > 0, b > 0 and n, m, k is natural numbers):

1. ⁿ√a b = ⁿ√a · ⁿ√b
   
   
2. $\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}$
   
   
3. $(\sqrt[n]{a})^k=\sqrt[n]{a^k}$
   
   
4. $\sqrt[n]{\sqrt[m]{a}}=\sqrt[nm]{a}$
   
   
5. $\sqrt[nk]{a^k}=\sqrt[n]{a}$
   
   
6. $\sqrt[n·k]{a^{m·k}}=(\sqrt[n]{a^m})$
   
   

7. $\sqrt[n]{a^n}=$	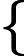	|a|	if n – even
   		a	if n – odd

   
   
8. For any a and b, such that 0 ≤ a ≤ b truly following inequality:
   ⁿ√ a  ≤ ⁿ√ b