Coplanar vectors
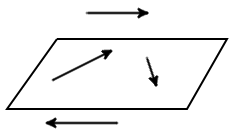 |
| Fig. 1 |
It is always possible to find a plane parallel to the two random vectors, in that any two vectors are always coplanar.
Condition of vectors coplanarity
- For 3-vectors. The three vectors are coplanar if their scalar triple product is zero.
- For 3-vectors. The three vectors are coplanar if they are linearly dependent.
- For n-vectors. Vectors are coplanar if among them no more than two linearly independent vectors.
Examples of tasks
Solution: calculate a scalar triple product of vectors
| a · [b × с] = | 1 | 2 | 3 | = |
| 1 | 1 | 1 | ||
| 1 | 2 | 1 |
= 1·1·1 + 1·1·2 + 1·2·3 - 1·1·3 - 1·1·2 - 1·1·2 = 1 + 2 + 6 - 3 - 2 - 2 = 2
Answer: vectors are not coplanar as their scalar triple product is not zero.
Solution: calculate a scalar triple product of vectors
| a · [b × с] = | 1 | 1 | 1 | = |
| 1 | 3 | 1 | ||
| 2 | 2 | 2 |
= 1·2·3 + 1·1·2 + 1·1·2 - 1·2·3 - 1·1·2 - 1·1·2 = 6 + 2 + 2 - 6 - 2 - 2 = 0
Answer: vectors are coplanar as their scalar triple product is zero.
Solution: Find the number of linearly independent vectors, for this we write the values of the vectors in a matrix and run at her elementary transformations
| 1 | 1 | 1 | ~ | ||
| 1 | 2 | 0 | |||
| 0 | -1 | 1 | |||
| 3 | 3 | 3 |
from 2 row we subtract the 1-th row; from 4 row we subtract the 1-th row multiplied by 3;
| ~ | 1 | 1 | 1 | ~ | 1 | 1 | 1 | ~ | ||||
| 1 - 1 | 2 - 1 | 0 - 1 | 0 | 1 | -1 | |||||||
| 0 | -1 | 1 | 0 | -1 | 1 | |||||||
| 3 - 3 | 3 - 3 | 3 - 3 | 0 | 0 | 0 |
for 3 row add 2 row
| ~ | 1 | 1 | 1 | ~ | 1 | 1 | 1 | ||||
| 0 | 1 | -1 | 0 | 1 | -1 | ||||||
| 0 + 0 | -1 + 1 | 1 + (-1) | 0 | 0 | 0 | ||||||
| 3 - 3 | 3 - 3 | 3 - 3 | 0 | 0 | 0 |
Since there are two non-zero row, then among the given vectors only two linearly independent vectors.
Answer: vectors are coplanar since there only two linearly independent vectors.
Add the comment