Vector projection
Page Navigation:
Definition. Projection of the vector AB on the axis l is a number equal to the value of the segment A1B1 on axis l, where points A1 and B1 are projections of points A and B on the axis l (Fig. 1).
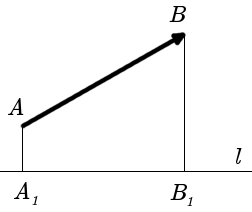 |
| Fig. 1 |
Definition. The vector projection of a vector a on a nonzero vector b is the orthogonal projection of a onto a straight line parallel to b.
Vector projection - formula
The vector projection of a on b is the unit vector of b by the scalar projection of a on b:
| proj ba = | a · b | b |
| |b|2 |
The scalar projection of a on b is the magnitude of the vector projection of a on b.
| |proj ba| = | a · b |
| |b| |
Examples of tasks
Examples of plane tasks
Example 1. Find the projection of vector a = {1; 2} on vector b = {3; 4}.
Solution:
Calculate dot product of these vectors:
a · b = 1 · 3 + 2 · 4 = 3 + 8 = 11Calculate the magnitude of vector b:
|b| = √32 + 42 = √9 + 16 = √25 = 5Calculate vector projection:
| proj ba = | a · b | b = | 11 | {3; 4} ={1.32; 1.76} |
| |b|2 | 25 |
Calculate scalar projection:
| |proj ba| = | a · b | = | 11 | = 2.2 |
| |b| | 5 |
Examples of spatial tasks
Example 2. Find the projection of vector a = {1; 4; 0} on vector b = {4; 2; 4}.
Solution:
Calculate dot product of these vectors:
a · b = 1 · 4 + 4 · 2 + 0 · 4 = 4 + 8 + 0 = 12Calculate the magnitude of vector b:
|b| = √42 + 22 + 42 = √16 + 4 + 16 = √36 = 6Calculate vector projection:
| proj ba = | a · b | b = | 12 | {4; 2; 4} = { | 4 | ; | 2 | ; | 4 | } |
| |b|2 | 36 | 3 | 3 | 3 |
Calculate scalar projection:
| |proj ba| = | a · b | = | 12 | = 2 |
| |b| | 6 |
Vectors
Vectors Definition. Main information
Component form of a vector with initial point and terminal point
Length of a vector
Direction cosines of a vector
Equal vectors
Orthogonal vectors
Collinear vectors
Coplanar vectors
Angle between two vectors
Vector projection
Addition and subtraction of vectors
Scalar-vector multiplication
Dot product of two vectors
Cross product of two vectors (vector product)
Scalar triple product (mixed product)
Linearly dependent and linearly independent vectors
Decomposition of the vector in the basis
Add the comment
