Vectors Definition. Main information
Page Navigation:
Vector definition
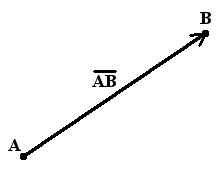
Definition. Vector is a directed line segment, ie the segment having a length and a definite direction. Graphically vector depicted as a directed line segments of a certain length. (Fig. 1)
 |
| Fig. 1 |
Vector designation
The vector which has a beginning point A and end point B, denoted AB (Fig. 1). Also, the vector represent one small letter, for example a.a.
Vector length
Definition. The length of the directed segment determines the numerical value of the vector and is called the length of the vector AB.
The length of the vector AB is denoted as: |AB|.
Zero vector
Definition. Zero vector is a vector whose start and end points coincide.
The zero vector is usually is denoted as 0.
The length of the zero vector is zero.
Collinear vectors
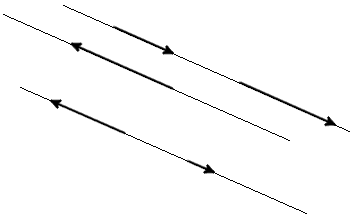
Definition. Vector parallel to one line or lying on one line are called collinear vectors (Fig. 2).
 |
| Fig. 2 |
Codirected vectors
Definition. Two collinear vectors a and b are called codirected vectors if their directions are the same: a↑↑b (Fig. 3).
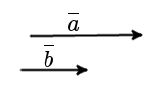 |
| Fig. 3 |
Oppositely directed vectors
Definition. Two collinear vectors a and b are called oppositely directed vectors if their directions are opposite: a↑↓b (Fig. 4).
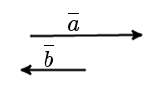 |
| Fig. 4 |
Coplanar vectors
Definition. Vectors parallel to the same plane, or lie on the same plane are called coplanar vectors (Fig. 5).
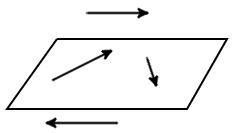 |
| Fig. 5 |
It is always possible to find a plane parallel to the two random vectors, in that any two vectors are always coplanar.
Equal vectors
Definition. Vectors a and b is an equal vectors if they are in the same or parallel lines, their directions are the same and the lengths are equal (Fig. 6).
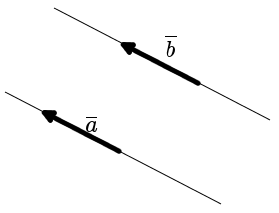 |
| Fig. 6 |
Two vectors are equal if they are collinear, codirected and have the same length:
a = b, if a↑↑b and |a| = |b|.
Unit vector
Definition. Unit vector or orth is a vector whose length is equal to one.
Vectors
Vectors Definition. Main information
Component form of a vector with initial point and terminal point
Length of a vector
Direction cosines of a vector
Equal vectors
Orthogonal vectors
Collinear vectors
Coplanar vectors
Angle between two vectors
Vector projection
Addition and subtraction of vectors
Scalar-vector multiplication
Dot product of two vectors
Cross product of two vectors (vector product)
Scalar triple product (mixed product)
Linearly dependent and linearly independent vectors
Decomposition of the vector in the basis
Add the comment
