OnlineMSchool
Study of mathematics online.
Study math with us and make sure that "Mathematics is easy!"
Sign in Log in Log out

Rectangle. Formulas and Properties of a Rectangle

Page Navigation: Definition of a rectangle The basic properties of a rectangle The sides of a rectangle The diagonal of a rectangle The perimeter of a rectangle The area of a rectangle The circumscribed circle of a rectangle (circumcircle) The angle between the side and diagonal The angle between the diagonals
Definition.
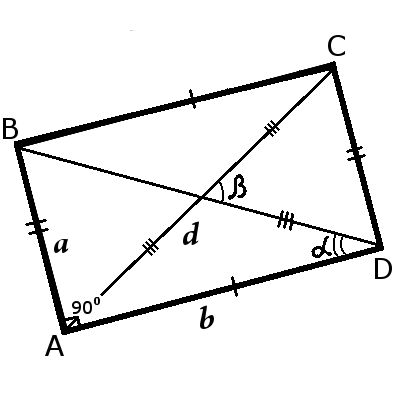
Rectangle - is a quadrilateral in which two opposite sides are equal and all angles is right.

Rectangles differ only ratio of long side to short but four angles is right, that is 90 degrees.

The sides of the rectangle is both its altitudes.

Image of a rectangle Image of a rectangle
Fig.1 Fig.2

The basic properties of a rectangle

Rectangle can be a parallelogram, rhombus or square in which all the angles right.
1. An opposite sides of the rectangle are the same length, i.e. they are equal:

AB = CD,   BC = AD
2. An opposite sides of the rectangle are parallel:

AB||CD,   BC||AD
3. An adjacent sides of the rectangle are always perpendicular:

AB ┴ BC,   BC ┴ CD,   CD ┴ AD,   AD ┴ AB
4. All four angles of the rectangle is right:

∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
5. The sum all of the angles of a rectangle is equal to 360 degrees:

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
6. A diagonals of the rectangle are equal:

AC = BD
7. The sum of the squares two diagonals is equal to the sum of the squares of the sides:

2d2 = 2a2 + 2b2
8. The each diagonal divides the rectangle into two equal shape, namely a right triangle.
9. A diagonal of a rectangle in half divides each other:

         AO = BO = CO = DO =  d
2
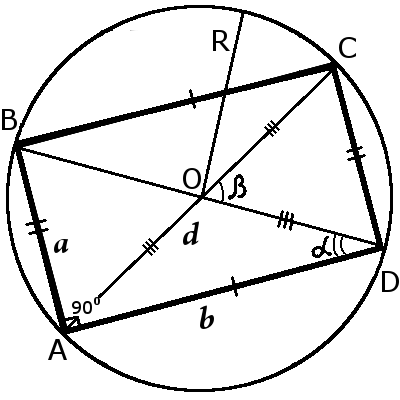
10. Intersection point of the diagonals is called the center of the rectangle and also a center of the circumcircle (incenter).
11. Diagonal of a rectangle is the diameter of the circumcircle.
12. Around the rectangle can always describe a circle, because the sum of the opposite angles is 180 degrees:

∠ABC + ∠CDA = 180°   ∠BCD + ∠DAB = 180°
13. In rectangle with the different size of sides never enter the incircle.

A rectangle sides

Definition.
The length of rectangle is called the length of the longer pair of its sides. The width of rectangle is called the length of the shorter pair of its sides.

A rectangle sides formulas:

1. Formula of rectangle sides in terms of diagonal and another rectangle side:
a = √d2 - b2
b = √d2 - a2
2. Formula of rectangle sides in terms of area and another rectangle side:
a = A
b
b = A
a
3. Formula of rectangle sides in terms of perimeter and another rectangle side:
a = P - 2b
2
b = P - 2a
2
4. Formula of rectangle sides in terms of diagonal and angle α:
a = d sinα
b = d cosα
5. Formula of rectangle sides in terms of diagonal and angle β:
a = d sin β
2
b = d cos β
2

The diagonal of a rectangle

Definition.
The diagonal of a rectangle is any segment that connects two opposite vertices of a rectangle.

Diagonal of a rectangle formulas:

1. Formula of rectangle diagonal in terms of rectangle sides (by the Pythagorean theorem)::
d = √a2 + b2
2. Formula of rectangle diagonal in terms of square and rectangle side:
d = √A2 + a4 = √A2 + b4
ab
3. Formula of rectangle diagonal in terms of perimeter and rectangle side:
d = √P2 - 4Pa + 8a2 = √P2 - 4Pb + 8b2
22
4. Formula of rectangle diagonal in terms of radius of the escribed circle (excircle):
d = 2R
5. Formula of rectangle diagonal in terms of diameter of the escribed circle (excircle):
d = Dc
6. Formula of rectangle diagonal in terms of sine of the angle that adjacent to the diagonal and the opposite side of the angle:
d = a
sin α
7. Formula of rectangle diagonal in terms of cosine of the angle that adjacent to the diagonal and the adjacent side of the angle:
d = b
cos α
8. Formula of rectangle diagonal in terms of sine of the acute angle between the diagonals and the area of a rectangle
d = √2A : sin β

The perimeter of a rectangle

Definition.
The perimeter of a rectangle is the sum of the lengths of all rectangle sides.

Perimeter of a rectangle formulas

1. Formula of rectangle perimeter in terms of rectangle sides:
P = 2a + 2b

P = 2(a + b)
2. Formula of rectangle perimeter in terms of area and rectangle side:
P = 2A + 2a2 = 2A + 2b2
ab
3. Formula of rectangle perimeter in terms of diagonal and rectangle side:
P = 2(a + √d2 - a2) = 2(b + √d2 - b2)
4. Formula of rectangle perimeter in terms of radius of the escribed circle (excircle) and rectangle side:
P = 2(a + √4R2 - a2) = 2(b + √4R2 - b2)
5. Formula of rectangle perimeter in terms of diameter of the escribed circle (excircle) and rectangle side:
P = 2(a + √Dc2 - a2) = 2(b + √Dc2 - b2)

The area of a rectangle

Definition.
The area of a rectangle the space is restricted rectangle sides or within the perimeter of a rectangle.

Area of a rectangle formulas

1. Formula of rectangle area in terms of rectangle sides:
A = a · b
2. Formula of rectangle area in terms of perimeter and rectangle side:
A = Pa - 2a2 = Pb - 2b2
22
3. Formula of rectangle area in terms of diagonal and rectangle side:
A = a√d2 - a2 = b√d2 - b2
4. Formula of rectangle area in terms of sine of the acute angle between the diagonals and the diagonal of a rectangle:
A = d2 · sin β
2
5. Formula of rectangle area in terms of radius of the escribed circle (excircle) and rectangle side:
A = a√4R2 - a2 = b√4R2 - b2
6. Formula of rectangle area in terms of diameter of the escribed circle (excircle) and rectangle side:
A = a√Dc2 - a2 = b√Dc2 - b2

The circumscribed circle of a rectangle (circumcircle)

Definition.
The circumscribed circle of a rectangle (circumcircle) circle which passes only four vertex of the angle and has a center at the intersection of the diagonals of the rectangle.

Radius of a rectangle formulas:

1. Formula of rectangle circumscribed radius in terms of rectangle sides:
R = √a2 + b2
2
2. Formula of rectangle circumscribed radius in terms of perimeter and rectangle side:
R = √P2 - 4Pa + 8a2 = √P2 - 4Pb + 8b2
44
3. Formula of rectangle circumscribed radius in terms of area and rectangle side:
R = √AS2 + a4 = √S2 + b4
2a2b
4. Formula of rectangle circumscribed radius in terms of diagonal:
R = d
2
5. Formula of rectangle circumscribed radius in terms of diameter of the escribed circle (excircle):
R = Dc
2
6. Formula of rectangle circumscribed radius in terms of sine of the angle that adjacent to the diagonal and the opposite side of the angle:
R = a
2sin α
7. Formula of rectangle circumscribed radius in terms of cosine of the angle that adjacent to the diagonal and the adjacent side of the angle:
R = b
2cos α
8. Formula of rectangle circumscribed radius in terms of sine of the acute angle between the diagonals and the area of a rectangle:
R = √2A : sin β
2

An angle between the diagonal and rectangle side

An angle between the diagonal and rectangle side formulas

1. Formula of angle between the diagonal and rectangle side in terms of diagonal and rectangle side:
sin α = a
d
cos α = b
d
2. Formula of angle between the diagonal and rectangle side in terms of angle between the diagonals:
α = β
2

An angle between the rectangle diagonals

An angle between the rectangle diagonals formulas:

1. Formula of angle between the rectangle diagonals in terms of angle between the diagonal and rectangle side:
β = 2α
2. Formula of angle between the rectangle diagonals in terms of area and rectangle diagonal:
sin β = 2A
d2
Geometry formulas Square. Formulas and Properties of a Square Rectangle. Formulas and Properties of a Rectangle Parallelogram. Formulas and Properties of a Parallelogram Rhombus. Formulas and Properties of a Rhombus Circle, disk, segment, sector. Formulas and properties Ellipse. Formulas and properties of ellipse Cylinder. Formulas and properties of a cylinder Cone. Formulas, characterizations and properties of a cone Area. Formulas of area Perimeter. Formulas of perimeter Volume. Formulas of volume Surface Area Formulas
All tables and Formulas

Add the comment

0
Follow OnlineMSchool on