Equation of a line

General form of a line equation

Any equation of a line on plane can by written in the general form

A x + B y + C = 0

where A and B are not both equal to zero.

Slope intercept form of a line equation

The general equation of a line when B ≠ 0 can be reduced to the next form

y = k x + b

where k is the slope of the line and b is the y-intercept. Slope of the line is equal to the tangent of the angle between this line and the positive direction of the x-axis. The y-coordinate is the location where line crosses the y-axis.

k = tg φ

Equation of the line passing through two different points on plane

If the line passes through two points A(x₁, y₁) and B(x₂, y₂), such that x₁ ≠ x₂ and y₁ ≠ y₂, then equation of line can be found using the following formula

x - x1	=	y - y1
x2 - x1		y2 - y1

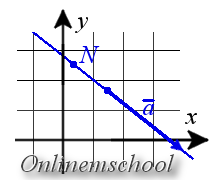
Parametric equations of a line on plane

Parametric equation of the line can be written as

	x = l t + x0
	y = m t + y0

where N(x₀, y₀) is coordinates of a point that lying on a line, a = {l, m} is coordinates of the direction vector of line.

Canonical equation of a line on plane

If you know the coordinates of the point A(x₀, y₀) If you know the coordinates of the point n = {l; m}, then the equation of the line can be written in the canonical form using the following formula

x - x0	=	y - y0
l		m

Example 1. Find the equation of a line passing through two points A(1, 7) and B(2, 3).

Solution. We use the formula for the equation of a straight line passing through two points

x - 12 - 1 = y - 73 - 7

From this equation, we express y in terms of x

x - 11 = y - 7-4

Find the Slope intercept form of line equation.

Multiply equations by -4.

y - 7 = -4(x - 1)

y = -4x + 11

Find the Parametric equations of this line

We use MN as direction vector of line.

MN = {2 - 1; 3 - 7} = {1; -4}

We use coordinates of point М in parametric equations of line

x = t + 1y = -4t + 7

Example 2. Find the equation of a line passing through two points M(1, 3) and N(2, 3).

Solution. It is impossible to use Equation of the line passing through two different points, since M_y - N_y = 0.

Find the Parametric equations of this line. We use MN as direction vector of line.

MN = {2 - 1; 3 - 3} = {1; 0}

We use coordinates of point М in parametric equations of line

x = t + 1y = 3

Equation of the line passing through two different points in space

If the line passes through two points A(x₁, y₁, z₁) and B(x₂, y₂, z₂), such that x₁ ≠ x₂, y₁ ≠ y₂ and z₁ ≠ z₂, then equation of line can be found using the following formula

x - x1	=	y - y1	=	z - z1
x2 - x1		y2 - y1		z2 - z1

Parametric equations of a line in space

Parametric equation of the line can be written as

	x = l t + x0
	y = m t + y0
	z = n t + z0

where (x₀, y₀, z₀) is coordinates of a point that lying on a line, {l; m; n} is coordinates of the direction vector of line.

Canonical equation of a line in space

If you know the coordinates of the point A(x₀, y₀, z₀) that lies on the line and the direction vector of the line n = {l; m; n}, then the equation of the line can be written in the canonical form using the following formula.

x - x0	=	y - y0	=	z - z0
l		m		n

Straight line as crossings of two planes

If the line is the intersection of two planes, then the equation of line can be found as the solution of the following system of equations

	A1x + B1y + C1z + D1 = 0
	A2x + B2y + C2z + D2 = 0

on condition that there has not been equality

A1	=	B1	=	C1	.
A2		B2		C2