Distance from a point to a line - 3-Dimensional.
Distance from a point to a line in space formula
If M0(x0, y0, z0) point coordinates, s = {m; n; p} directing vector of line l, M1(x1, y1, z1) - coordinates of point on line l, then distance between point M0(x0, y0, z0) and line l can be found using the following formula:
| d = | |M0M1×s| |
| |s| |
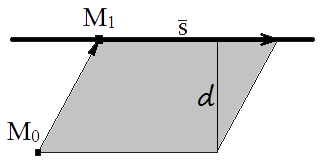
Proof of the formula of distance from a point to a line for the space problem
If l is line equation then s = {m; n; p} is directing vector of line, M1(x1, y1, z1)is coordinates of point on line. From properties of cross product it is known that the module of cross product of vectors is equal to the area of a parallelogramme constructed on these vectors
A = |M0M1×s|.
On the other hand parallelogramme area is equal to product of its side on height spent to this side
A = |s|d.
Having equated the areas it is simple to receive the formula of distance from a point to a line.
Examples of tasks with from a point to a line in space
| x - 3 | = | y - 1 | = | z + 1 |
| 2 | 1 | 2 |
Solution.
From line equation find:
s = {2; 1; 2} - directing vector of line;
M1(3; 1; -1) - coordinates of point on line.
Then
M0M1 = {3 - 0; 1 - 2; -1 - 3} = {3; -1; -4}
| M0M1×s = | i | j | k | = |
| 3 | -1 | -4 | ||
| 2 | 1 | 2 |
= i ((-1)·2 - (-4)·1) - j (3·2 - (-4)·2) + k (3·1 -(-1)·2) = {2; -14; 5}
| d = | |M0M1×s| | = | √22 + (-14)2 + 52 | = | √225 | = | 15 | = 5 |
| |s| | √22 + 12 + 22 | √9 | 3 |
Answer: distance from point to line is equal to 5.
Add the comment
