Angle between line and plane
Angle between line and plane formula
If in space given the direction vector of line L
s = {l; m; n}
and equation of the plane
Ax + By + Cz + D = 0,
then the angle between this line and plane can be found using this formula
| sin φ = | | A · l + B · m + C · n | |
| √A2 + B2 + C2 · √l2 + m2 + n2 |
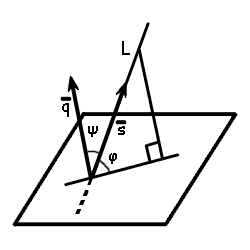
Proof of the formula of angle between line and plane
From the equation of line can be found directing vector of the line has form
s = {l; m; n}From the equation of a plane the normal vector of the plane has form
q = {A; B; C}From the formula of scalar product of vectors find the cosine of the angle between the normal vector and direction vector
| cos ψ = | | q · s | |
| | s | · |q | |
Since φ = 90° - ψ, then the sine of the angle between the line and the plane is sin φ = cos ψ.
Using the formula of the scalar product of vectors and module of vectors in coordinate form, we obtain the formula for calculating the angle between the line and the plane.
Examples of tasks with angle between line and plane
| x - 4 | = | y + 2 | = - | z - 6 |
| 2 | 6 | 3 |
Solution.
From the equation of the line we find the direction vector
s = {2; 6; -3}From the equation of the plane we find the normal vector
q = {1; -2; 3}Using the formula, we find the angle between the line and the plane
| sin φ = | | 2 · 1 + 6 · (-2) + (-3) · 3 | | = |
| √22 + 62 + (-3)2 · √12 + (-2)2 + 32 |
| sin φ = | | 2 - 12 - 9 | | = | 19 | = | 19 |
| √4 + 36 + 9 · √1 + 4 + 9 | √49 · √14 | 7√14 |
| Answer: |
|
Add the comment
