Distance between two planes
Page navigation:
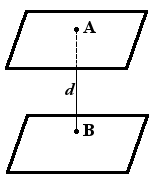
Definition. The distance between two planes is equal to length of the perpendicular lowered from a point on a plane.
Distance between two planes formula
If Ax + By + Cz + D1 = 0 and Ax + By + Cz + D2 = 0 is a plane equation, then distance between planes can be found using the following formula
| d = | |D2 - D1| |
| √A2 + B2 + C2 |
Examples of tasks with distance between two planes
Example 1.
To find distance between planes 2x + 4y - 4z - 6 = 0 and x + 2y - 2z + 9 = 0.
Solution. Let's check up, whether planes are parallel, for this purpose we will multiply the equation of the second plane on 2
2x + 4y - 4z + 18 = 0As planes are parallel than for calculation distance between planes we use the formula:
| d = | |18 - (-6)| | = | |24| | = | 24 | = 4 |
| √22 + 42 + (-4)2 | √36 | 6 |
Answer: distance from plane to plane is equal to 4.
Analytic geometry: Introduction and contentsDistance between two pointsMidpoint. Coordinates of midpointEquation of a lineEquation of a planeDistance from point to planeDistance between two planesDistance from a point to a line - 2-DimensionalDistance from a point to a line - 3-DimensionalAngle between two planesAngle between line and plane
Add the comment
