Distance between two points
Page navigation:
Definition. Distance between two points is the length of the line segment that connects this points.
Distance formulas:
- The formula for calculating the distance between two points A(xa, ya) and B(xb, yb) on plane:
AB = √(xb - xa)2 + (yb - ya)2 - The formula for calculating the distance between two points A(xa, ya, za) and B(xb, yb, zb) in space:
AB = √(xb - xa)2 + (yb - ya)2 + (zb - za)2
Proof of the formula of distance between two points for the plane problem
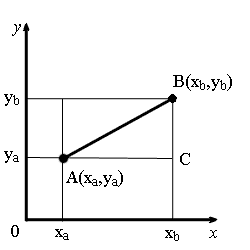
From the points A and B drop perpendiculars to the coordinate axes.
Consider a right triangle ∆ABC. Legs of the triangle are equal to:
BC = yb - ya.
Using the Pythagorean theorem, calculate the length of the hypotenuse AB:
Substituting to this expression the lengths of AC and BC which expressed in terms of the coordinates of points A and B, we obtain the formula for calculating the distance between points on the plane.
Proof of the formula for calculating the distance between two points in space is similar.
Examples of tasks with distance between two points
Examples of tasks with distance between two points on 2D
Example 1.
Find the distance between two points A(-1, 3) and B(6,2).
Solution.
Answer: AB = 5√2.
Example 2.
Find the distance between two points A(0, 1) and B(2,-2).
Solution.
AB = √(xb - xa)2 + (yb - ya)2 = √(2 - 0)2 + (-2 - 1)2 = √22 + (-3)2 = √13
Answer: AB = √13.
Examples of tasks with distance between two points on 3D
Example 3.
Find the distance between two points A(-1, 3, 3) and B(6, 2, -2).
Solution.
= √(6 - (-1))2 + (2 - 3)2 + (-2 - 3)2 = √72 + 12 + 52 = √75 = 5√3
Answer: AB = 5√3.
Example 4.
Find the distance between two points A(0, -3, 3) and B(3, 1, 3).
Solution.
AB = √(xb - xa)2 + (yb - ya)2 + (zb - za)2 =
= √(3 - 0)2 + (1 - (-3))2 + (3 - 3)2 = √32 + 42 + 02 = √25 = 5
= √(3 - 0)2 + (1 - (-3))2 + (3 - 3)2 = √32 + 42 + 02 = √25 = 5
Answer: AB = 5.
Analytic geometry: Introduction and contentsDistance between two pointsMidpoint. Coordinates of midpointEquation of a lineEquation of a planeDistance from point to planeDistance between two planesDistance from a point to a line - 2-DimensionalDistance from a point to a line - 3-DimensionalAngle between two planesAngle between line and plane
Add the comment
