Square of the sum

• Square of the sum - definition
• Derivation of the formula of square of the sum
• Applying of square of the sum formula
• Geometric illustration
• Examples of task

The square of the sum of two expressions is equal to the square of the first, plus twice the product of the first and second, plus the square of the second:

(a + b)² = a² + 2ab + b²

The proof of the formula is very simple. To prove the formula is sufficient to multiply the expression:

Square of the sum formula convenient to use:

• to disclose the brackets
• to simplify expressions
• to calculate the squares of large numbers without using a calculator or multiplication in column

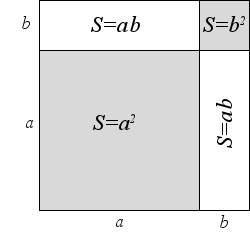
Formula of square of the sum of two positive integers a and b can be illustrate a geometrically.

Consider a square with side (a + b), its area is (a + b)².

Subdivided this square into four parts by straight lines.

Two of the parts are gray squares with the side sizes a and b. Areas of two smaller squares are a² and b² respectively.

Two other parts are congruent white rectangles with the side sizes a and b each. The area of each of the two rectangles is ab

Then area of the large square is the sum of the areas of its parts, the Figure illustrates the square of the sum formula:

Expand brackets (x + 3)².

Solution: Apply the square of the sum formula.

Expand brackets (2x + 3y²)².

Solution: Apply the square of the sum formula.

Simplify the expression 9x² + 6x + 1(3x + 1).

Solution: Apply the square of the sum formula in numerator.

Apply the square of the sum formula to calculate 71².

Solution: