Cylinder Area Calculator
This free online calculator will help you to find the area of a cylinder surface.
Using this online calculator, you will receive a detailed step-by-step solution to your problem, which will help you understand the algorithm how to find cylinder surface area.
Calculation of Cylinder Area
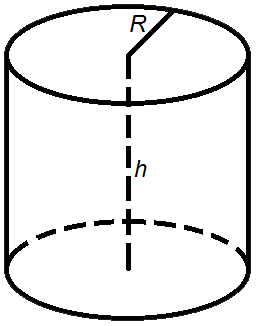Enter the value of radius and height of the cylinder
| R = |
| h = |
You can input only integer numbers, decimals or fractions in this online calculator (-2.4, 5/7, ...). More in-depth information read at these rules.
Try online calculators for calculation of geometrical figures surface areaArea of cubeArea of rectangular prism (cuboid)Area of cylinderArea of coneArea of sphereShow all online calculators
Try online calculators for calculation of geometrical figures volumeVolume of cubeVolume of prismVolume of rectangular prism (cuboid)Volume of parallelepipedVolume of pyramidVolume of tetrahedronVolume of sphereVolume of cylinderVolume of coneShow all online calculators
Add the comment