Cone. Formulas, characterizations and properties of a cone
Page Navigation:
Definition of a cone
Elements of a cone
Volume of a cone
Surface area of a cone
Equation of a cone
Basic properties of a cone
Definition.
Cone is geometric body which is formed by a set of rays from apex (vertex) point and cross any flat surface, and at the intersection form basis of the cone.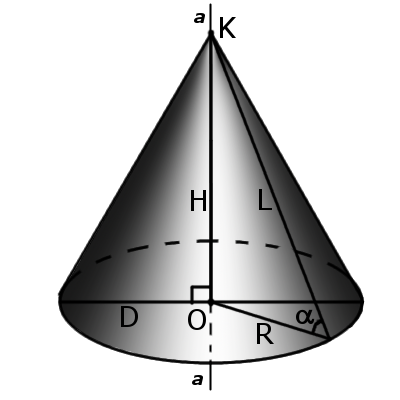 |
 |
|
| Fig.1 | Fig.2 | |
 |
 |
|
| Fig.3 | Fig.4 |
Elements of a cone
Definition. Apex (vertex) of a cone is a point (K) of which overlook rays.
Definition. Base of a cone is plane is formed as a result of crossing the flat surface and all radiation emanating from the apex cone. In the cone may include a base such as circle, ellipse, parabola and hyperbole.
Definition. Lateral height (L) of a right circular cone is the distance from any point on the circle to the apex of the cone.
Formula. Lateral height of right circular cone in terms of radius R and height H (by the Pythagorean theorem):
L = √R2 + H2
Definition. Guide curve of a cone is a curve, which describes the base of circuit cone.
Definition. Lateral side of a cone is the set of all generatrix cone. That is, the surface of which is formed by movement of generatrix on the guide curve of a cone
Definition. Surface area of a cone consisting of the lateral surface of cone and bases.
Definition.Height of a cone (H) is segment, which comes from the vertex cone and perpendicular to its base.
Definition. Axis of a cone (a) is a line passing through the vertex cone and center of the base.
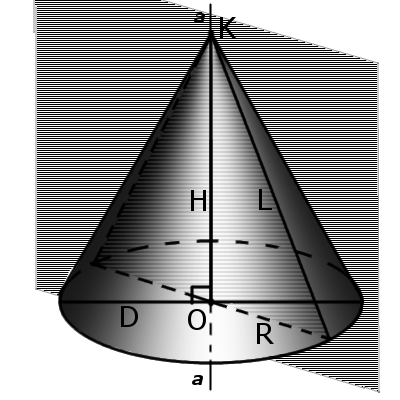 Definition. Axial section of the cone is cone-sectional plane that passes through the axis of the cone. This section forms an isosceles triangle whose sides are formed by generatrix and the base of the triangle is a diameter of base of cone.
Definition. Axial section of the cone is cone-sectional plane that passes through the axis of the cone. This section forms an isosceles triangle whose sides are formed by generatrix and the base of the triangle is a diameter of base of cone.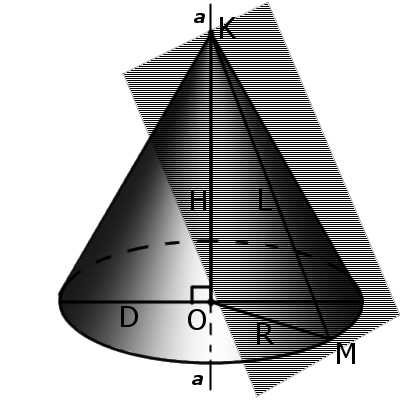 Definition. Tangent plan to cone is a plane passing through generatrix cone and perpendicular to the axial cone section.
Definition. Tangent plan to cone is a plane passing through generatrix cone and perpendicular to the axial cone section.Definition. Cone based on the circle, ellipse, parabola or hyperbole respectively called circular, elliptical, hyperbolic or parabolic cone (the last two have infinite volume).
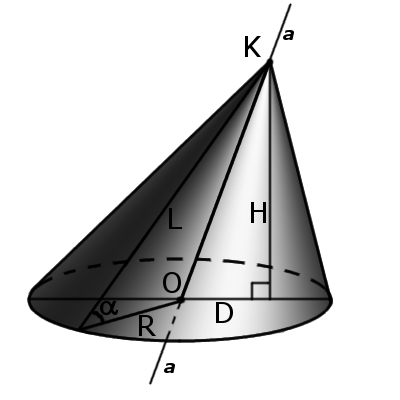
 Definition. Right cone is a cone whose axis is perpendicular to the base. In such a cone axis coincides with the height and all generatrix equal.
Definition. Right cone is a cone whose axis is perpendicular to the base. In such a cone axis coincides with the height and all generatrix equal.Formula. Volume of circular cone:
where R - base radius, а H - cone height.
| V = | 1 | πHR2 |
| 3 |
Formula. Area lateral side (Al) of right cone in term of radius R and generatrix length L:
Al = πRL
Formula. The total surface area (At) a right circular in terms of radius R and generatrix length L:
At = πRL + πR2
 Definition. Oblique cone is cone whose axis is not perpendicular to the base. In such a cone axis does not coincide with the height.
Definition. Oblique cone is cone whose axis is not perpendicular to the base. In such a cone axis does not coincide with the height.
Formula. The volume of any cone:
where A - base area and H - cone height.
| V = | 1 | AH |
| 3 |
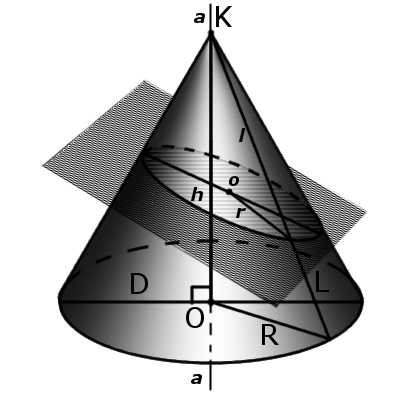
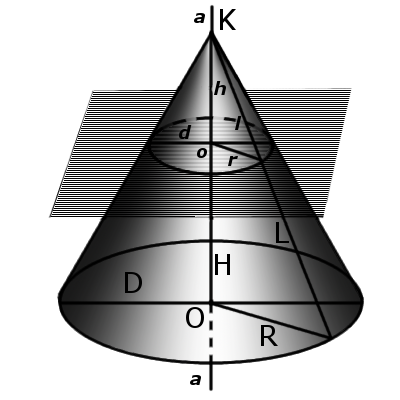 Definition. Truncated cone is part of cone which is located between the base cone and the plane of intersection cone.
Definition. Truncated cone is part of cone which is located between the base cone and the plane of intersection cone.Formula. Volume of truncated cone:
where A1 and A2 - area smaller base and larger base respectively, H and h the distance from the top cone (apex) to the center of the lower and upper bases, respectively.
| V = | 1 | (A2H - A1h) |
| 3 |
Equation cone
1. The equation of the right circular cone with center at the origin the Cartesian coordinate system (x, y, z):
| x2 | + | y2 | - | z2 | = 0 |
| a2 | b2 | c2 |
2. The equation of the right elliptical cone with center at the origin the Cartesian coordinate system (x, y, z):
| x2 | + | y2 | = | z2 |
| a2 | b2 | c2 |
Basic properties of a cone
1. All generators directly cone are equal.
2. When rotating a right triangle around his cathetus at 360 ° formed right circular cone.
3. When rotating isosceles triangle around its axis 180 ° formed right circular cone.
4. At the intersection of cone plane is parallel to the base cone formed a circle. (See. Truncated cone).
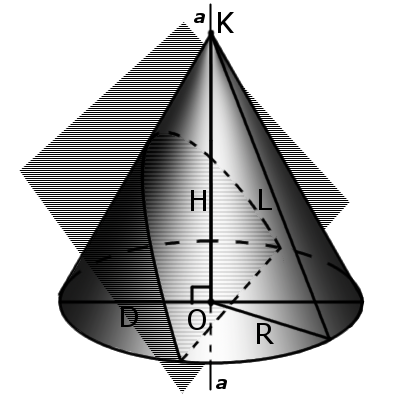
5. If the intersection of the plane is not parallel on cone and not overlap with the base is formed at the intersection ellipse (Fig. 3).
6. If the plane of section passing through the base is formed at the intersection of parabola (Fig. 4).
7. If the plane passes through the top section then the intersection formed an isosceles triangle (see. Axial section).
8. The center of gravity of any cone is one fourth the height of the center of the base.
Geometry formulas
Square. Formulas and Properties of a Square
Rectangle. Formulas and Properties of a Rectangle
Parallelogram. Formulas and Properties of a Parallelogram
Rhombus. Formulas and Properties of a Rhombus
Circle, disk, segment, sector. Formulas and properties
Ellipse. Formulas and properties of ellipse
Cylinder. Formulas and properties of a cylinder
Cone. Formulas, characterizations and properties of a cone
Area. Formulas of area
Perimeter. Formulas of perimeter
Volume. Formulas of volume
Surface Area Formulas
Add the comment
