Area Formulas for Geometric Figures
Area of a triangle formulas
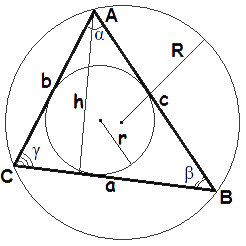
- Area of a triangle when we know the base and the height
The area of a triangle is equal to half of base times height.
A = 1 a · h 2 - Area of a triangle when we know the lengths of all three of its sides
Heron's formula
A = √s(s - a)(s - b)(s - c) - Area of a triangle when we know two sides and the included angle
The area of a triangle is equal to half of a product of two sides and sine of the angle between this sides.
A = 1 a · b · sin γ 2 A = 1 a · c · sin β 2 A = 1 b · c · sin α 2 - Area of a triangle when we know three sides and circumradius
A = a · b · с 4R - Area of a triangle when we know semiperimeter and in-radiuswhere A - the area of a triangle,
The area of a triangle is equal to semiperimeter times in-radius.
A = s · r
a, b, c - the length of sides BC,AC,AB accordingly,
h - the height, the length of the altitude,
α, β, γ - the angles,
r - the length of the in-radius,
R - the length of the circumradius,
s = a + b + c - the semiperimeter, or half of the triangle's perimeter. 2
Area of a square formulas
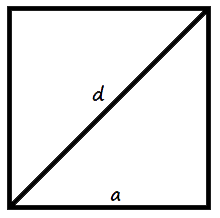
- Area of a square when we know the length of a side
The area of a square is equal to squared side.
A = a2 - Area of a square when we know the length of diagonalwhere A - the area of a square,
The area of a square is half of squared diagonal.
A = 1 d2 2
a - the lenth of side,
d - the length of diagonal.
Area of a rectangle formula
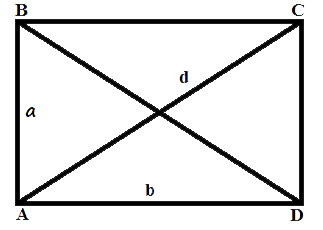
a, b - the length of sides(the height and width of rectangle).
Area of a parallelogram formulas
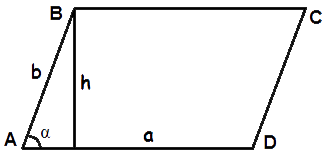
- Area of a parallelogram when we know the side and the height
The area of a parallelogram is equal to side times height.
A = a · h - Area of a parallelogram when we know two sides and the included angle
The area of a parallelogram is equal to a product of two sides and sine of the angle between this sides.
A = a · b · sin α
where A - the area of a parallelogram,
a, b - lengths of sides,
h - the height, the length of the altitude,
α - the measure of the angle between sides.
Area of a rhombus formulas
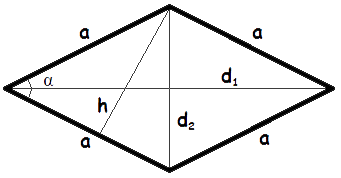
- Area of a rhombus when we know the side and the height
The area of a rhombus is equal to side times height.
A = a · h - Area of a rhombus when we know length of a side and the included angle
The area of a rhombus is equal to a product of the squared side and sine of the angle between sides of a rhombus.
A = a2 · sin α - Area of a rhombus when we know length of its diagonalswhere A - the area of a rhombus,
The area of a rhombus is equal to half a product of it diagonals lengths.
A = 1 d1 · d2 2
a - the length of a side,
h - the height, the length of the altitude,
α - the measure of the angle between sides of a rhombus,
d1, d2 - the length of diagonals.
Area of a trapezium formulas
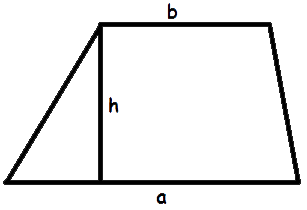
- Heron's formula for a trapezium
A = a + b √(s-a)(s-b)(s-a-c)(s-a-d) |a - b| - Area of a trapezium when we know length of 2 bases and the heightwhere A - the area of a trapezium,
The area of a trapezium is equal to product of the height and half-sum of two bases
A = 1 (a + b) · h 2
a, b - the length of the 2 bases,i.e., the parallel sides,
c, d - length of the legs (the lateral sides),
s = a + b + c + d - the semiperimeter, or half of the trapezium's perimeter. 2
Area of a quadrangle formulas
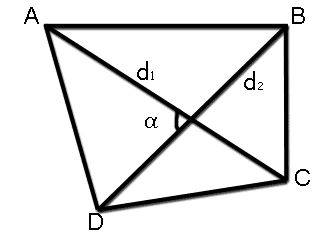
- Area of a quadrangle when we know length of its diagonals and angle between diagonals
The area of a quadrangle is equal to product of its diagonals and and sine of the angle between diagonals
A = 1 d1 d2 sin α 2
where A - the area of a quadrangle,
d1, d2 - the length of diagonals,
α - the angle between diagonals. - Area of a quadrangle when we know length of its perimeter and in-radius
The area of a quadrangle is equal to perimeter timesin-radius
A = s · r 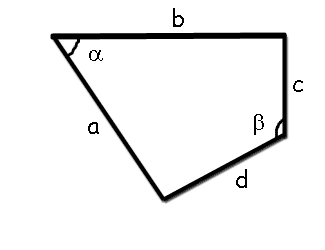 Area of a quadrangle when we know length of its sides and value of opposite cornerswhere A -the area of a quadrangle,A = √(s - a)(s - b)(s - c)(s - d) - abcd cos2θ
Area of a quadrangle when we know length of its sides and value of opposite cornerswhere A -the area of a quadrangle,A = √(s - a)(s - b)(s - c)(s - d) - abcd cos2θ
a, b, c, d - the length of sides,
s = a + b + c + d - semiperimeter of quadrangle, 2 θ = α + β - half the sum of two opposite angles of a quadrilateral. 2
Area of a circle formulas

- Area of a circle when we know its radius
The area of a circle is equal to a product of squared radius and pi.
A = π r2 - Area of a circle when we know its diameterwhere A - the area of a circle,
The area of a circle is equal to a quarter product of squared diameter and pi.
A = 1 π d2 4
r - the length of the radius,
d - the length of the diameter.
Area of a ellipse formulas
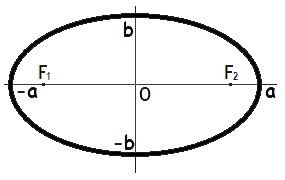
a - the length of the major semiaxis,
b - the length of the minor semiaxis,
Add the comment

 Triangle
Triangle Square
Square Rectangle
Rectangle Parallelogram
Parallelogram Rhombus
Rhombus Trapezium
Trapezium Quadrangle
Quadrangle Circle
Circle Ellipse
Ellipse