Cylinder. Formulas and properties of a cylinder
Page Navigation:
Definition of a cylinder
Elements of a cylinder
Right circular cylinder
Volume of a cylinder
Surface area of a cylinder
Oblique cylinder
Slanted cylinder
Definition.
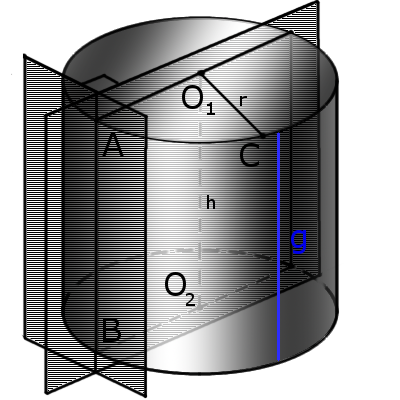
Cylinder is a geometric body that limited cylindrical surface and two planes, called basics of cylinder (top and bottom).A cylindrical surface is a surface obtained by moving a straight line (generatrix) parallel to itself, along a flat curve.
The cylinder bases are plane figures formed by the intersection of a cylindrical surface with two planes.
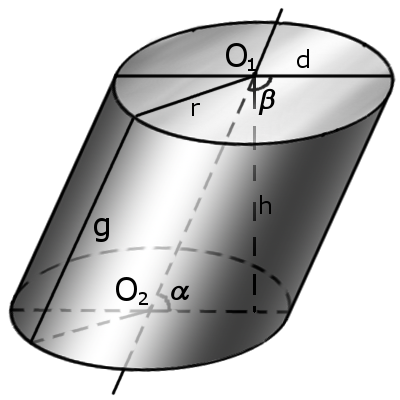
Definition. Generatrix of cylinder g is a combination of all segments parallel (AB), which connect the cylinder bases.
 |
 |
 |
||
| Fig. 1 | Fig. 2 | Fig. 3 |
Right circular cylinder
Commonly the word cylinder is understood to refer to a finite section of a right circular cylinder having a finite height with circular ends perpendicular to the axis.
Right circular cylinder described as a three-dimensional shape that is formed by rotating of rectangle on its side at 360°. In this case formed a right circular cylinder with a circle at the base of the cylinder.
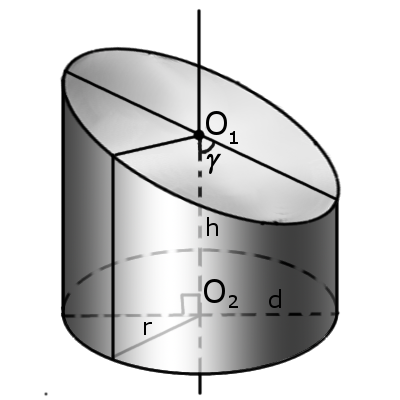
Definition. Radius of cylinder r of the cylinder is a radius of bases.
Definition. Diameter of cylinder d is a diameter of bases.
Definition. Height of cylinder h is a distance between the bases of the cylinder.
Definition. Axis is a line passing through the centers of the cylinder bases.
Definition. Surface area consisting of side area (lateral area), top area and bottom area.
Definition. Axis section is a section of the cylinder plane passing through the axis of the cylinder.
Definition. Tangent plan to the cylinder is a plane passing through the generatrix of the cylinder and perpendicular to the axial section of the cylinder.
Formula. Volume of a cylinder:
where r is a radius of the base, h is height of a cylinder, d is diameter of the base.
| V = πr2h = π | d2 | h , |
| 4 |
Formula. Lateral area (Al) in terms of the radius and height:
Al = 2πrh = πdh
Formula. Surface area (As) in terms of the radius and height:
As = 2πr(h + r)
If the bases (top and bottom surfaces) are not parallel the cylinder called oblique (Fig.2).
If the foundations are not perpendicular to the height the cylinder called slanted (Fig.3).
Geometry formulas
Square. Formulas and Properties of a Square
Rectangle. Formulas and Properties of a Rectangle
Parallelogram. Formulas and Properties of a Parallelogram
Rhombus. Formulas and Properties of a Rhombus
Circle, disk, segment, sector. Formulas and properties
Ellipse. Formulas and properties of ellipse
Cylinder. Formulas and properties of a cylinder
Cone. Formulas, characterizations and properties of a cone
Area. Formulas of area
Perimeter. Formulas of perimeter
Volume. Formulas of volume
Surface Area Formulas
Add the comment
