Ellipse. Formulas, elements and properties of an ellipse
Definition of ellipse
Elements of ellipse
Properties of ellipse
Equations of ellipse
Inscribed circle (incircle) of ellipse
Exscribed circle (excircle) of ellipse
Area of ellipse
Area of the ellipse segment
Circumference of ellipse
Arc of ellipse
Definition of an ellipse
Definition.
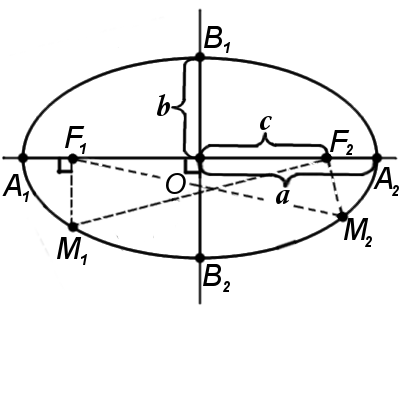
Ellipse is a closed curve around two different points (focal points F1 and F2) in a plane such that the sum of the distances from the two focal points is constant for every point (Mn) on the curve.
F1M1 + F2M1 = F1M2 + F2M2 = A1A2 = const
 |
 |
|
| Fig.1 | Fig.2 |
Elements of ellipse
F1 и F2 - focal points of ellipse
Axes of ellipse.
А1А2 = 2a - major axis (larger direct that crosses focal points F1 and F2)
B1B2 = 2b - minor axis (smaller direct that perpendicular to major axis and intersect it at the center of the ellipse О)
a - semi-major axis
b - semi-minor axis
O - center of the ellipse
Vertices of ellipse A1, A2, B1, B2
Diameter of ellipse - is any straight line segment that passes through the center of the ellipse and whose endpoints lie on the ellipse.
Linear eccentricity c - is the distance from the focal point to the center of the ellipse.
Eccentricity of ellipse e is the ratio of the linear eccentricity c to the length of the semi-major axis a. The eccentricity of an ellipse always be 0 < e < 1, the eccentricity of the circle is e = 0, the eccentricity of the parabola is e = 1, the eccentricity of the hyperbola is e > 1.
| e = | c |
| a |
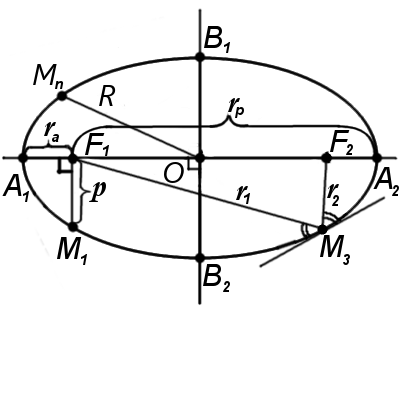
Focal radius of ellipse r1, r2 is a distances from point on ellipse to focal point.
Radius of an ellipse R - is a distance from ellipse the center to point (Мn) at ellipse.
де e - eccentricity, а φ - the angles within the radius (R) and major axis A1A2.
| R = | ab | = | b |
| √a2sin2φ + b2cos2φ | √1 - e2cos2φ |
де e - eccentricity, а φ - the angles within the radius (R) and major axis A1A2.
Focal parameter of ellipse p - is the focal radius that perpendicular to ma axis:
| p = | b2 |
| a |
Flattening (ellipticity) of ellipse (oblateness) k is a measure of the compression of a circle along a semi-minor axis. Since the semi-minor axis of the ellipse is always smaller then semi-major axis, then k < 1, and for circle k = 1:
f = 1 - √1 - e2,
where e - eccentricity.
| f = | a - b |
| a |
where e - eccentricity.
Directrix of ellipse (1 - k ) is a line parallel to the minor axis and no touch to the ellipse. The distance from any point M on the ellipse to the focus F is a constant fraction of that points perpendicular distance to the directrix, resulting in the equality p/e.
Properties of ellipse
1. Angle betwin tangent and focal radius r1 is equal to angle betwin tangent and focal radius r2 (Fig. 2, point М3).
2. Equations of tangent in point М with coordinates (xM, yM):
| 1 = | xxM | + | yyM |
| a2 | b2 |
3. If two parallel lines cross the ellipse than the distance that conect the midle point of a segment this lines will cross the center of the ellipse.
4. Evolute is the asteroid that stretched along the long axis.
5. If the inscribe the ellipse with foci F1 and F2 in any triangle ∆ ABC than:
| 1 = | F1A ∙ F2A | + | F1B ∙ F2B | + | F1C ∙ F2C |
| CA ∙ AB | AB ∙ BC | BC ∙ CA |
Equations of ellipse
Canonical equations of ellipse:
The ellipse can be described in Cartesian coordinate system if the center O of the ellipse locate in origin coordinate axis, than:
If the center of the ellipse O is located in point with coordinates (xo, yo), than:
| 1 = | x2 | + | y2 |
| a2 | b2 |
| 1 = | (x - xo)2 | + | (y - yo)2 |
| a2 | b2 |
Parametric equations of ellipse:
| { | x = a cos α | де 0 ≦ α < 2π |
| y = b sin α |
Inscribed circle of ellipse
A circle inscribe in the ellipse touch to two vertices B1 and B2. Thereby, inradius r the same like semi-minor axis OB1:
r = b
Exscribed circle of ellipse
A circle exscribe the ellipse touch to two vertices A1 and A2. Thereby, exradius R the same like semi-major axis OA1:
R = a
Area of ellipse
Formulas definition of ellipse area:
S = πab
Area of ellipse segment
Arc segment area at the left side of chord with coordinates (x, y) and (x, -y):
| S = | πab | - | b | ( | x | √ | a2 - x2 + a2 ∙ arcsin | x | ) |
| 2 | a | a |
Circumference of ellipse (perimeter approximation)
The circumference (C) of ellipse is very difficult to calculate. Below formula an approximation that is within about ~0,63% of the true value:
| C ≈ 4 | πab + (a - b)2 |
| a + b |
Arc of ellipse
Formulas definition length of an arc of an ellipse:
1. Parametric form the length of an arc of an ellipse in terms of semi-major axisa and semi-minor axis b:
| t2 | ||
| l = | ∫ | √a2sin2t + b2cos2t dt |
| t1 |
2. Parametric form the length of an arc of an ellipse in terms of semi-major axis a and eccentricity e:
| t2 | ||
| l = | ∫ | √1 - e2cos2t dt, e < 1 |
| t1 |
Geometry formulas
Square. Formulas and Properties of a Square
Rectangle. Formulas and Properties of a Rectangle
Parallelogram. Formulas and Properties of a Parallelogram
Rhombus. Formulas and Properties of a Rhombus
Circle, disk, segment, sector. Formulas and properties
Ellipse. Formulas and properties of ellipse
Cylinder. Formulas and properties of a cylinder
Cone. Formulas, characterizations and properties of a cone
Area. Formulas of area
Perimeter. Formulas of perimeter
Volume. Formulas of volume
Surface Area Formulas
Add the comment
