Equal vectors

Page Navigation:

Equal vectors - definition
Conditions of vectors equality
Examples of tasks
- plane tasks
- spatial tasks

Definition. Vectors a and b is an equal vectors if they are in the same or parallel lines, their directions are the same and the lengths are equal (Fig. 1).

Two vectors are equal if they are collinear, codirected and have the same length:

a = b, if a↑↑b and |a| = |b|.

Conditions of vectors equality.Vectors are equal if their coordinates are equal.

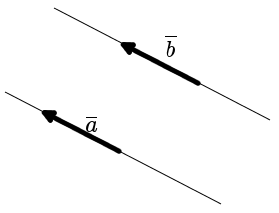Fig. 1

Examples of tasks

Examples of plane tasks

Example 1. Determine which of the vectors are equal a = {1; 2}, b = {1; 2}, c = {3; 2}.

Solution:

a = b - as their coordinates are equal,
a ≠ c - as their coordinates are not equal,
b ≠ c - as their coordinates are not equal.

Example 2. At what value of the parameter n the vectors a = {1; 8;} and b = {1; 2n} are equal.

Solution:

Verify the equality of components of vectors
a_x = b_x = 1
a_y = b_y => 8 = 2n => n = 8/2 = 4

Answer: when n = 4 vectors a and b are equal.

Examples of spatial tasks

Example 3. Determine which of the vectors are equal a = {1; 2; 4}, b = {1; 2; 2}, c = {1; 2; 4}.

Solution:

a = c - as their coordinates are equal,
a ≠ b - as their coordinates are not equal,
b ≠ c - as their coordinates are not equal.

Example 4. At what value of the parameter n the vectors a = {1; 2; 4} and b = {1; 2; 2n} are equal.

Solution:

Verify the equality of components of vectors
a_x = b_x = 1
a_y = b_y = 2
a_z = b_z => 4 = 2n => n = 4/2 = 2

Answer: when n = 2 vectors a and b are equal.

Vectors Vectors Definition. Main information Component form of a vector with initial point and terminal point Length of a vector Direction cosines of a vector Equal vectors Orthogonal vectors Collinear vectors Coplanar vectors Angle between two vectors Vector projection Addition and subtraction of vectors Scalar-vector multiplication Dot product of two vectors Cross product of two vectors (vector product) Scalar triple product (mixed product) Linearly dependent and linearly independent vectors Decomposition of the vector in the basis

Online calculators with vectors

Tasks and exercises with vector 2D

Tasks and exercises with vector 3D

Add the comment