Collinear vectors

Page Navigation:

Definition.

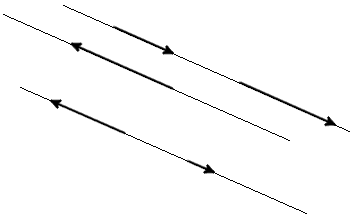Vector parallel to one line or lying on one line are called collinear vectors (Fig. 1).

Fig. 1

Condition of vectors collinearity

Two vectors are collinear, if any of these conditions done:

Condition of vectors collinearity 1. Two vectors a and b are collinear if there exists a number n such that

a = n · b

Condition of vectors collinearity 2. Two vectors are collinear if relations of their coordinates are equal.

N.B. Condition 2 is not valid if one of the components of the vector is zero.

Condition of vectors collinearity 3. Two vectors are collinear if their cross product is equal to the zero vector.

N.B. Condition 3 applies only to three-dimensional (spatial) problems.

The proof of the condition of collinearity 3

Let there are two collinear vectors a = {a_x; a_y; a_z} and b = {na_x; na_y; na_z}. We find their cross product

a × b =	i	j	k	= i (a_yb_z - a_zb_y) - j (a_xb_z - a_zb_x) + k (a_xb_y - a_yb_x) =
	a_x	a_y	a_z
	b_x	b_y	b_z

= i (a_yna_z - a_zna_y) - j (a_xna_z - a_zna_x) + k (a_xna_y - a_yna_x) = 0i + 0j + 0k = 0

Examples of tasks

Examples of plane tasks

Example 1. Which of the vectors a = {1; 2}, b = {4; 8}, c = {5; 9} are collinear?

Solution: Since the vectors does not contain a components equal to zero, then use the condition of collinearity 2, which in the case of the plane problem for vectors a and b will view:

a_x	=	a_y	.
b_x		b_y

Means:

Vectors a and b are collinear because	1	=	2	.
	4		8

Vectors a and с are not collinear because	1	≠	2	.
	5		9

Vectors с and b are not collinear because	5	≠	9	.
	4		8

Example 2. Prove that the vector a = {0; 3} and b = {0; 6} are collinear.

Solution: Since the vector components contain zero, then use the condition of collinearity 1, we find there is a number n for which:

b = na.

For this we find a nonzero component of vector a in this case this is a_y. If the vectors are collinear then

n =	b_y	=	6	= 2
	a_y		3

Calculate the value of na:

na = {2 · 0; 2 · 3} = {0; 6}

Since b = 2a, the vectors a and b are collinear.

Example 3. Find the value of n at which the vectors a = {3; 2} and b = {9; n} are collinear.

Solution: Since the vectors does not contain a components equal to zero, then use the condition of collinearity 2

a_x	=	a_y	.
b_x		b_y

Means:

3	=	2	.
9		n

Solve this equation:

n =	2 · 9	= 6
	3

Answer: vectors a and b are collinear when n = 6.

Examples of spatial tasks

Example 4. Which of the vectors a = {1; 2; 3}, b = {4; 8; 12}, c = {5; 10; 12} are collinear?

Solution: Since the vectors does not contain a components equal to zero, then use the condition of collinearity 2, which in the case of the plane problem for vectors a and b will view:

a_x	=	a_y	=	a_z	.
b_x		b_y		b_z

Means:

Vectors a and b are collinear because	1	=	2	=	3	.
	4		8		12

Vectors a and с are not collinear because	1	=	2	≠	3	.
	5		10		12

Vectors с and b are not collinear because	5	=	10	≠	12	.
	4		8		12

Example 5. Prove that the vector a = {0; 3; 1} and b = {0; 6; 2} are collinear.

Solution: Since the vector components contain zero, then use the condition of collinearity 1, we find there is a number n for which:

b = na.

For this we find a nonzero component of vector a in this case this is a_y. If the vectors are collinear then

n =	b_y	=	6	= 2
	a_y		3

Calculate the value of na:

na = {2 · 0; 2 · 3; 2 · 1} = {0; 6; 2}

Since b = 2a, the vectors a and b are collinear.

Example 6. Find the value of n and m at which the vectors a = {3; 2; m} and b = {9; n; 12} are collinear.

Solution: Since the vectors does not contain a components equal to zero, then use the condition of collinearity 2

a_x	=	a_y	=	a_z	.
b_x		b_y		b_z

Means:

3	=	2	=	m
9	=	n	=	12

From this relations we obtain two equations:

3	=	2
9	=	n

3	=	m
9	=	12

Solve this equations:

n =	2 · 9	= 6
	3

m =	3 · 12	= 4
	9

Answer: vectors a and b are collinear when n = 6 and m = 4.

Vectors Vectors Definition. Main information Component form of a vector with initial point and terminal point Length of a vector Direction cosines of a vector Equal vectors Orthogonal vectors Collinear vectors Coplanar vectors Angle between two vectors Vector projection Addition and subtraction of vectors Scalar-vector multiplication Dot product of two vectors Cross product of two vectors (vector product) Scalar triple product (mixed product) Linearly dependent and linearly independent vectors Decomposition of the vector in the basis

Online calculators with vectors

Tasks and exercises with vector 2D

Tasks and exercises with vector 3D

Add the comment