Orthogonal vectors
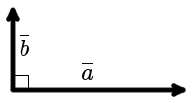 |
| рис. 1 |
Examples of tasks
Examples of plane tasks
In the case of the plane problem for the vectors a = {ax; ay} and b = {bx; by} orthogonality condition can be written by the following formula:
Solution:
Calculate the dot product of these vectors:
a · b = 1 · 2 + 2 · (-1) = 2 - 2 = 0Answer: since the dot product is zero, the vectors a and b are orthogonal.
Solution:
Calculate the dot product of these vectors:
a · b = 3 · 7 + (-1) · 5 = 21 - 5 = 16Answer: since the dot product is not zero, the vectors a and b are not orthogonal.
Solution:
Calculate the dot product of these vectors:
a · b = 2 · n + 4 · 1 = 2n + 42n + 4 = 0
2n = -4
n = -2
Answer: vectors a and b are orthogonal when n = -2.
Examples of spatial tasks
In the case of the plane problem for the vectors a = {ax; ay; az} and b = {bx; by; bz} orthogonality condition can be written by the following formula:
Solution:
Calculate the dot product of these vectors:
a · b = 1 · 2 + 2 · (-1) + 0 · 10 = 2 - 2 + 0 = 0Answer: since the dot product is zero, the vectors a and b are orthogonal.
Solution:
Calculate the dot product of these vectors:
a · b = 2 · 3 + 3 · 1 + 1 · (-9) = 6 + 3 -9 = 0Answer: since the dot product is zero, the vectors a and b are orthogonal.
Solution:
Calculate the dot product of these vectors:
a · b = 2 · n + 4 · 1 + 1 · (-8)= 2n + 4 - 8 = 2n - 42n - 4 = 0
2n = 4
n = 2
Answer: vectors a and b are orthogonal when n = 2.
Add the comment
