Scalar triple product
Page Navigation:
Definition. Scalar triple product of vectors (vector product) is a dot product of vector a by the cross product of vectors b and c.
Scalar triple product formula
Scalar triple product of vectors is equal to the determinant of the matrix formed from these vectors.
Scalar triple product of vectors a = {ax; ay; az}, b = {bx; by; bz} and c = {cx; cy; cz} in the Cartesian coordinate system can be calculated using the following formula:
| a · [b × c] = | ax | ay | az |
| bx | by | bz | |
| cx | cy | cz |
Scalar triple product properties
- Geometric interpretation.Module of scalar triple product of vectors a, b and c is equal to the volume of the parallelepiped formed by these vectors:
Vparallelepiped = |a · [b × c]|
- Geometric interpretation.The volume of the pyramid formed by three vectors a, b and c is equal to one-sixth of the modulus of the scalar triple product of this vectors:
Vpyramid = 1 |a · [b × c]| 6 - If the mixed product of three non-zero vectors equal to zero, these vectors are coplanar.a · [b × c] = b · (a · c) - c · (a · b)a · [b × c] = b · [c × a] = c · [a × b] = -a · [c × b] = -b · [a × c] = -c · [b × a]a · [b × c] + b · [c × a] + c · [a × b] = 0 - Jacobi identity.
Scalar triple product examples
Example 1. Find the scalar triple product of vectors a = {1; 2; 3}, b = {1; 1; 1}, c = {1; 2; 1}.Solution:
a · [b × с] = 1 2 3 = 1 1 1 1 2 1
= 1·1·1 + 1·1·2 + 1·2·3 - 1·1·3 - 1·1·2 - 1·1·2 = 1 + 2 + 6 - 3 - 2 - 2 = 2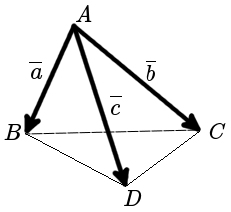
Example 2.Find the volume of a pyramid constructed on vectors a = {1; 2; 3}, b = {1; -1; 1}, c = {2; 0; -1}.Solution: Calculate scalar triple product of vectors:
a · [b × с] = 1 2 3 = 1 -1 1 2 0 -1
= 1·(-1)·(-1) + 2·1·2 + 3·1·0 - 3·(-1)·2 - 2·1·(-1) - 1·1·0 =
= 1 + 4 + 0 + 6 + 2 - 0 = 13Calculate the volume of the pyramid using the following properties:
Vpyramid = 1 |a · [b × c]| = 13 = 2 1 6 6 6 Vectors Vectors Definition. Main information Component form of a vector with initial point and terminal point Length of a vector Direction cosines of a vector Equal vectors Orthogonal vectors Collinear vectors Coplanar vectors Angle between two vectors Vector projection Addition and subtraction of vectors Scalar-vector multiplication Dot product of two vectors Cross product of two vectors (vector product) Scalar triple product (mixed product) Linearly dependent and linearly independent vectors Decomposition of the vector in the basisAdd the comment
0
